Special thanks go to John Kineman who has acted as a reader for this blog, providing invaluable help in clarifying my thinking. I alone bear responsibility for the end result!
The need to surrender sovereignty, to compete effectively within turbulent environments, requires an organisation to manage dynamically the primary risks it faces in its relations to its customers (Hirschhorn 1999). Primary risk is the risk that the primary task relation in each customer situation has not been defined in a way that satisfies the ‘multi-sided’ demands arising within each customer’s context-of-use. The previous blogs argued that socio-technical open-systems approaches were not adequate for managing this kind of relational agility, nor were Darwinian notions of ‘survival of the fittest’ sufficient for describing the processes of mutual adaptation and section involved. In this blog the concept of agency in living biological systems is used to understand the nature of the dynamic relations to the environment that turbulence demands.
This need was for an approach that could account for the general property of adaptive behaviour in an organisation’s relations in turbulent environments. This meant that adaptation had to be a general property of the living system itself as a whole and not externally located in either regulatory or environmental systems. This required not only distinguishing technological material, sentient efficient and formal causes. It also meant addressing how these material, efficient and formal causes could themselves be subject to the selective pressures of final cause, and in so doing,, understand ‘sovereignty’ differently – as ‘agency’.
Understanding agency in living biological systems
Rosen sought to distinguish mechanisms from living systems (Rosen 1991), defining living systems as anticipatory in their relation to their environments (Rosen 1985). The anticipatory nature of a living system enabled it “to decouple the identity of the system, which must be environmentally independent, from its behaviors, which will of course vary from one environment to another.” (Rosen 2000: p278).[1] Rosen’s description of this kind of anticipatory behavior of biological systems culminated in ‘class 5 Universal Adaptive Systems’ because of their combining an adaptive model of the relation to the environment combined with adaptive sensory modalities (Rosen 1974).[2] In considering the possibilities for applying this thinking to social organizations, Rosen defined class 5 systems as “systems with an unlimited access to their medium that can establish correlations between any environmental quantity and the states of the controlled system, and function effectively in any medium.” What, then, were the characteristics of such living systems?
The relational structure of these living systems described the organization of relations between its possible behaviors that instituted behavioral closure with respect to its medium. Autopoiesis focused on the structural coupling of this relational structure with its medium and how it was conserved (Maturana and Varela 1980[1972]). Structural coupling referred to a two-way relation between the genotypes of living systems with their phenotypic behaviors, in which each living system was supporting the organization of the others. Luhmann pointed out (Luhmann 2013[2002]: pp83-101), however, that while structural coupling addressed co-ontogenic drift in these mutual effects arising as a side-effect of random mutations, it provided no basis for describing the processes of genotypic adaptation. Genotypic adaptation here referred to the way a living system could change its overall way of being structurally coupled in pursuit of better adaptation between itself and its medium. If we are to include genotypic adaptation in Rosen’s ‘Class 5 Universal Adaptive Systems’, autopoiesis alone is thus an insufficient basis for giving an account of such adaptation.
Describing agency in terms of living system identity
The work of Barandiaran et al built on the work of Maturana and Varela to define the agency of a living system as its “autonomous organization that adaptively regulates its coupling with its medium and contributes to sustaining itself as a consequence” (Barandiaran, Di Paolo, and Rohde 2009). Quoting from their work, the agency of a living system had three characteristics:
- Individuality and spatio-temporal asymmetry – there is a system as a distinguishable entity that is different from its environment. The system is constituted for itself as a reference point in space and time, not for an observer of the system (who can choose any reference point to its convenience and accommodate the observations accordingly).
- Interactional asymmetry – The system is doing something by itself in its environment. The organization of the system (from which norms emerge) is determining the modulation of its coupling with its environment. Given that the system depends on certain conditions defined by its organization, and that it modulates its coupling in relation to it, a deep sense of agency comes to the surface. The system is not only acting, but through its actions is maintaining and individuating itself.
- Normativity – the way the system does something by itself in its environment is according to a certain goal or norme. the way the system’s constitutive processes and its dependencies between the system and the environment affect self-maintenance.
Each of these three characteristics define a ‘cut’[3] defining an asymmetry between what is on either side of the ‘cut’. Rosen’s definition of a living system was in terms of a behavioral closure between metabolism, replication and repair (see Figure 3). Kineman extends this definition to include the system’s selection as a genotype with its phenotypic behavior, enabling its behavior to be described in terms of the asymmetry between what is on either side of each ‘cut’ (Kineman 2008)[4]. These three asymmetries are described below and shown in Figure 1, in which the blue and orange arrows describe relations across the ontic and epistemic ‘cuts’ respectively:
- Causal isolation arising from the existence of some form of causal boundary defined by the observer: “to the extent that interaction is delayed temporally or separated spatially, causation itself becomes more independent of the larger system (of interaction or observation)”. In these terms, aspects of the state space of the living system identified by the observer remain spatio-temporally The identity of the system as a living system is based on a causally isolating ‘cut’.
- Ontic assumptions implicit in the relations between encoding and decoding: “such relations that extend across the subject-object boundary (both sides of which may be present as perception, and also dissolved in action) must be treated as creative (i.e., ontological) information relations”. These assumptions define a state space for both the living system and for the medium with which it is structurally coupled.
- Epistemic assumptions implicit in the relations both within the causally isolated state space of the living system and within the state space of its structural coupling, they constrain the ways in which encoding and decoding relations are themselves related: “These relations are entirely contextual, existing in the ‘ambiance’ of any modeling relation.”[5] This leaves open the issue of whether the relation of the living system to its medium is lateral among structurally-coupled living systems within an ecosystem or is stratified through relations of embeddedness within nested living systems”[6].
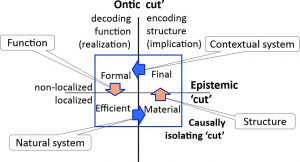
Figure 1: The system identity of a living system
An important distinction is made for living biological systems between the observed Natural system (the lower blue arrow in Figure 1) and the Contextual system (the upper blue arrow). The Natural system is the living system identified by the causally isolating ‘cut’ made by the observer. Kineman’s aim is to give an account of how the system is constituted for itself as a reference point in space and time, not for an observer of the system. The Contextual system is “that aspect of a Natural system that provides the conditions for existence of another system”, ‘another system’ being the living systems in the medium.
The other two orange arrows characterize modeling relations in the sense of Rosen and Kineman (see footnote 5). Structure is “an abstraction from nature of a ‘code’ in the form of a measurable patterns, which becomes the exemplary (i.e., instance of a) basis for a natural contextual model”, i.e., ‘structure’ referred to the genotypic characteristics of the living system within the context of its medium. Function is “the expression of a code from a contextual model as an attractive potential that drives processes via functions”, i.e., ‘function’ referred to the phenotypic characteristics of the living system’s behaviors per se.
An observer having identified a living system in terms of its causally isolating ‘cut’, therefore, the ontic and epistemic ‘cuts’ define four quadrants identified with Aristotle’s four causes (Aristotle 1996: p38 ff). With a living biological system, the Natural system is taken to be that which is observed to be causally isolated in nature, hence the above specialized uses of ‘structure’ and ‘function’(Kineman 2011). Given that the description of the Natural system is nevertheless in terms of observables and the relations between them, for example in this description of a Leaf System (Krupanidhi et al. 2017), each of the quadrants may be represented as a particular form of ‘closure’ in terms of category theory (Arbib and Manes 1975).[7] ‘Closure’ here refers to every node in the graph representation of each form of closure being reachable from somewhere else within the graph[8]. Again, quoting from (Kineman 2011):
- Efficient closure indicates a functional object, an agent of change.
- Material closure indicates a natural object, a material system with unique behavioral attributes.
- Final closure indicates an exemplary structural object or percept.[9]
- Formal closure indicates a final object, a selective template or model with implicit ends.
The blue and orange arrows in Figure 1 therefore summarize the relations between the four causes in terms of two different kinds of n-functor[10]. The first (the blue arrows) is within the localized and non-localized categories reflecting the behavioral characteristics of the Natural system and the effects of the selective pressures from the Contextual medium respectively. The second (the orange arrows) is between the localized and non-localized categories describing the way each constrains the possibilities open to the other.
The agency of a living system, then, defined as its “autonomous organization that adaptively regulates its coupling with its medium and contributes to sustaining itself as a consequence” (Barandiaran, Di Paolo, and Rohde 2009), is thus defined by Kineman in terms of the system identity of a living system defined by a circular causality between the four causes represented by the arrows in Figure 1: “Identity is thus a circular pairing of realized and contextual entailments. It is a single recursive causal hierarchy where each of the four components of the holon (system, context, structure, and function) form a closed loop defining a system (giving it identity).”
Kineman refers to the relations between the localized and the non-localized as functors (Kineman 2018), and follows Rosen (Rosen 1991: p89) in referring to the causal entailments between the efficient and material causes as “realized” and the inferential entailments between the final and formal causes as “contextual”.[11] As we see below, this system identity conserves the structural coupling of a living system through conserving not only the relations between these four closures, but also in their relation to the medium with which it is structurally coupled.[12]
The n-functors of a living system identity and their inverses
The circular causality between the four closures are indicated in Figure 1 by the direction of the arrows (and by the left-hand cycle in Figure 2), in which each arrow represents an n-functor i.e. a mapping between an n-category and its n-1-category (remembering that a category in category theory is a graph defined by its vertices and edges). The direction of these mappings is deductive, the behavioral closures at the ‘to’ end of the relation being constrained by the behavioral closures selected by the ‘from’ end, e.g., the behavioral closures of the efficient cause category is constrained by the form of the formal cause category. The text boxes in Figure 2 describe these deductive mappings. In contrast, the inverses of these n-functors (in the right-hand cycle in Figure 2) are inductive, i.e., what forms of material cause are induced by a final cause, what forms of efficient cause are induced by a material cause, what forms of formal cause are induced by an efficient cause, and what forms of final cause are induced by a formal cause.
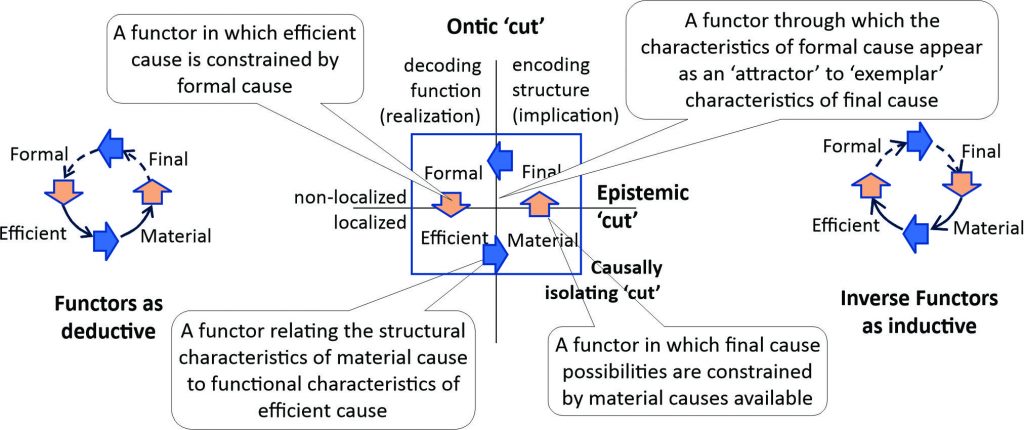
Figure 2: The living system identity
Returning to the definitions of behavioral closure in (Boxer 2023), the n-functors can be described using n-categories (Baez 1997)[13] (see Figure 2) to describe the stratified relations between them:
- a 1st order behavioral closure describes the behaviors of the category defined by the material cause closure as all the possible trajectories across the edges of the graph, each one of which will be an n+1 category with respect to the graph’s vertices that are n-category objects[14].
- a 2nd order behavioral closure describes the behaviors of the category defined by the efficient cause closure as all the possible ways of constraining the 1st order behavioral closures, the n+2 categories defined in terms of vertices corresponding to the 1st order behavioral closures in the n+1-category, and
- a 3rd order behavioral closure describes the behaviors of the category defined by the formal cause closure as all the possible way of constraining the 2nd order behavioral closures, the n+3 categories defined in terms of vertices corresponding to the 2nd order behavioral closures in the n+2 category.
In these terms, the n-functors in Figure 2 will be n-morphisms defining the relations between the n+1 and n+2 categories, i.e., n+2-morphisms, and between the n+2 and n+3 categories, i.e., n+3-morphisms. Considering these relations inductively in terms of inverse n-functors, the variety of possible 1st order behavioral closures constitute superposed states representing all the possible behaviors able to be realized by this living system, restricting the possible 3rd order behavioral closures that may be ‘chosen’. Within Figure 2, this is a diagonal relation between the material and formal cause closures in which the ‘choice’ of formal cause closure, within the context of the circular closure of the system as a whole, is from amongst the superposed set of possible material cause closures.
Sovereignty, then, is the relation of formal cause to final cause and to the other two causes, the effect of which involves choosing between possible superposed material states. But this ‘choosing’ is within the context of the circular causality reflecting the genotypic and phenotypic system identity of the living system. This still leaves open the question of how to render genotypic adaptation as a general property of the living system. Something is still missing in our account.
Distinguishing phenotypic and genotypic agency
To the circular relations between the n-functors in Figure 2 must be added the functors relating the living system to its medium. Figure 3 (Kineman 2018: Figure 6) shows the Metabolism-Repair (M-R) System of Rosen (Rosen 1991) that identifies three distinct phenotypic behavioral strategies by its components in relation to its environment (E/A): metabolism (F), replication (B) and repair (f). Repair is the sustaining of a particular way of organizing localized behavioral possibilities, replication is the ability to reproduce the way of organizing the localized behavioral possibilities, and metabolism is the transformational effects of behaviors. To these three Kineman added the fourth selection relation of the living system by its environment (E/f), the selective pressure for particular genotypic behaviors in support of the medium.
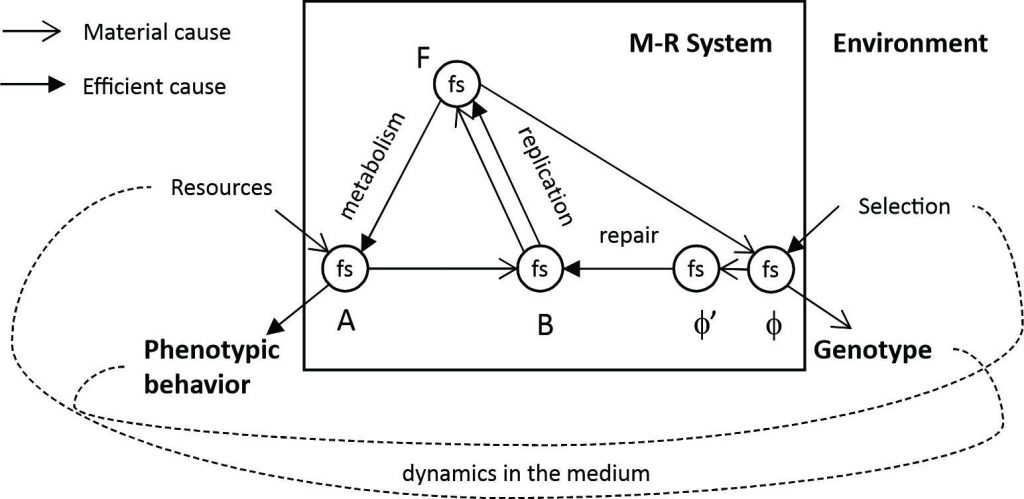
Figure 3: The relation of the Natural System to its environment
In the following quote, Kineman identifies four different forms of structural coupling to the medium, referring to a living system identity as a ‘holon’ to capture its ‘whole’ status, and to the functors described in this paper as ‘entailments’ (see footnote 11): “Thus there are four possible entailment arrows for each component and four internal elements. Each component and the larger system have self-similar holon organization as described above, where all interactive possibilities are closed with each other, except that the environment is part of that closure.” (Kineman 2018)
There are thus four different kinds of genotypic behavioral strategy that a living system may realize, depending on the way each of the four forms of causation is structurally coupled through inverse functors with a particular form of causation in the system identity of the living systems in its medium (the green arrows in Figure 4)[15].
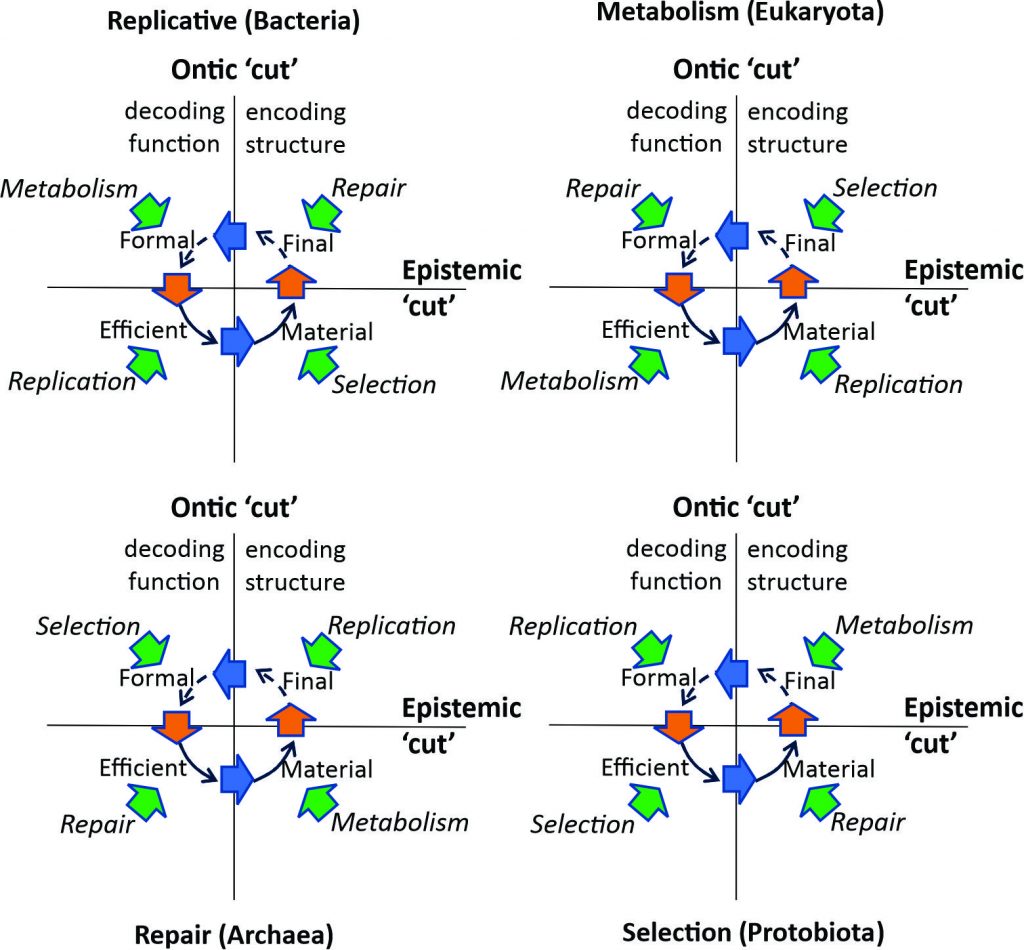
Figure 4: Four different kinds of behavioral strategy
Kineman shows how this structural coupling is present not only for efficient causation but in relation to all four causal closures. The functor relations of each causal category within a living system identity are thus also phenotypically coupled through inverse functor relations to the corresponding causal categories in each of the other living systems’ system identities with which it is structurally coupled (Kineman 2018).[16] These four ways in which this structural coupling is possible are represented in Figure 4 by the four different rotational alignments of the four phenotypic behaviors within each of the four quadrants. The resulting four types of behavioral strategy by a living system identity are named based on the inverse functor relating to efficient causation. The result is a descriptively rich account of the different kinds of behavioral strategies that a living system may take up within its medium (Kineman 2009).
The structural coupling with living systems in the medium in relation to which agency is exhibited is thus present phenotypically in all four quadrants as a general property of the living system. This agency is conserving autonomous organization through conserving a way of being in relation to the three ‘cuts’ with their three characteristics. It is a general property because there is no sub-system acting as a kind of central controller, regulating according to some fixed norm independent of the system’s current state and thereby acting as an external constraint on the system, reducing the system itself to a mechanism.[17]
This structural coupling of all four quadrants does more than describe phenotypic coupling, however, insofar as the medium is itself constituted by a holobiont that also exhibits system identity with its circular causation. With the medium as holobiont, the environment truly has ‘a life of its own’, the distinguishing characteristics of turbulent environments. This goes further than the identification of the ecological niche with the formal cause closure (Kineman 2009) to identify different granularities of identity closure within ecosystems per se (Ulanowicz 2000), the dynamics of which continue to implicate the way the three ‘cuts’ are held in relation to each other (Ulanowicz 2019)[18]. This allows us to consider there to be circular causality in the relations between the inverse functor relations impacting on each of the four causal closures.
This presence of circular causality in the medium gives rise to an environmentally-induced selection of behaviors – einselection – that is genotypic in its effects. In terms of Figure 2, this einselection may be represented by a diagonal relation between the efficient and final causes in which final cause, reflecting the environment’s constraining effects on all four causal closures, represent environmentally-induced selective pressures to which the possible efficient causes may respond. This einselection enables genotypic adaptation to be understood as a general property of the living system identity. It implies ‘a class 5 universal adaptive system’ exhibiting agency, following the direction of Rosen’s thinking, in which emergent modulations of constraints concerning the living system identity occur as a general property of the system in ways that are sensitive to both the norms defined by the system identity but also by the environment with which the living system is structurally coupled.
Surrendering sovereignty, then, involves inverse functors inducing effects across all aspects of a living system’s causal closure as a general property of its relation to its medium. It suggests that we need to look more closely at the general properties of the relations across the causally isolating ‘cut’ alongside the other two asymmetries used by Kineman to define a living system identity. I take up the relation across this third relational ‘cut’ in the next blog.
Notes
[1] The equivalent description of social systems by Ackoff and Emery was as purposeful systems that were multi-functional in their capabilities and independent of their environment in the way they used those capabilities. (Ackoff and Emery 1972).
[2] Classes 1 to 4 had lesser degrees of capacity to be anticipatory, having some combination of their functioning, their model of the environment and/or their sensory modalities, at least one of which was hard-wired i.e., non-adaptive. All five classes, however, were classes of living biological system.
[3] This ‘cut’ is the making of a distinction following (Spencer-Brown 1979[1969]: p1): “a distinction is drawn by arranging a boundary with separate sides so that a point on one side cannot reach the other side without crossing the boundary. … Once a distinction is drawn, the spaces, states, or contents on each side of the boundary, being distinct, can be indicated … There can be no distinction without motive, and there can be no motive unless contents are seen to differ in value.”
[4] In a joint paper with Béla A. Bánáthy, and Judith Rosen (Kineman, Bánáthy, and Rosen 2007), these three ‘cuts’ were identified with state-referential, referential and non-referential forms of information, “both referential and non-referential informational acts being constrained to (defined within) a state-determined frame of reference”.
[5] A ‘modeling relation’, following Rosen and Kineman, describes “a complementarity between descriptive and … prescriptive potentials of a system and their natural realizations; mediated by information relations” (Kineman 2011). ‘Natural realization’ refers to that which is observed in nature. This complementarity means that the modeling relations commute in the same way as the referred-to observations in nature (Rosen 2000: pp168-69).
[6] While these lateral relations would be between distinct living biological systems, these stratified relations of embeddedness arise within the context of holobionts (Singh et al. 2013; Gilbert 2012). It is in the context of these stratified relations of embeddedness that it becomes meaningful to speak of surrendering sovereignty, as argued in the previous blog.
[7] The ‘modeling relation’ is used in two senses, therefore, in this blog: first, as the relation of the non-localized to the localized; and second, as the relation of the category-theoretic graphs representing the observer’s understanding of each of the quadrants.
[8] Category theory was used by Rosen to formalize the nature of anticipatory systems (Rosen 1958: pp324-25).
[9] Kineman describes final cause in terms of “(1) exemplification; that is, a system’s use of prior phenomena to establish a goal or direction that may attract development of a system along a path to a defined end; (2) directional tendency toward a pre-defined result contextualized as an exemplar; (3) end-directedness built into a system model (a programmed result or goal direction)”.(Kineman 2011) [my italics] While (2) captures the emergent characteristics of how the system responds to selective pressures, (1) and (3) relate to the classes of system in (Rosen 1974), with (1) picking up on the role of memory and (3) picking up on the effects of sensory modalities.
[10] In category theory, a functor is a mapping between categories. These are n-functors relating an n-category to an n+1 category, inducing partial orderings (see (Baez 1997).
[11] Rosen is referring to non-localized inferential entailment between propositions and localized causal entailments between external events in order to identify impredicativity, i.e., self-referencing definition, in which each turns back on the other, instituting the defining characteristic of a living system (Rosen 2000: pp89-90).
[12] As will emerge in the next blog, the form that the living system identity arising from the circular relation between these four closures takes in relation to the living system’s medium is from the ‘internalist’ consistency of the system’s conservation of its identity (Van de Vijver 1998). This will be contrasted with an ‘architectural’ consistency of what are the identity-defining characteristics of the system’s behaviors, i.e., its behavioral strategy with respect to its medium, and an ‘externalist’ consistency of the behavioral characteristics of what the system ‘does’ for its medium, i.e., what kinds of ‘value’ it creates.
[13] In category theory, n-categories are a way of thinking about stratification or embeddedness. Let simplicial complex X represent a category in which the vertices of simplicial complex X are objects and a simplex is a particular set of relations between these objects. If the objects of this simplicial complex are themselves sets of relations between vertices defining a simplicial complex Y, where this simplicial complex Y is also representing a category, then if simplicial complex Y is representing an n-category, then simplicial complex X is representing an n+1-category. Objects in the n-category Y are thus embedded in the objects in the n+1-cagtegory X and the relation between the n+1-category X and n-category Y is one of stratification .
[14] In category theory, the vertices in this n-category are monoidal categories, making n=0.
[15] These inverse functors are between n-categories of the same dimensionality but which still induce partial orderings in the behavioral closures of the corresponding causal closure.
[16] Another way of thinking about the effects of reverse functors is in terms of entanglement between the causal closures of the living systems.
[17] The Viable Systems Model is based on the role of such ‘external’ sub-systems in its systems one to five (Beer 1981).
[18] The conservation of the relational ‘cut’ is here identified with ‘agency’, the ontic ‘cut’ represents being subject to the laws of physics, and the epistemic ‘cut’ represents the relation to entropy.
References
Ackoff, Russell L., and Fred E. Emery. 1972. On Purposeful Systems (Tavistock Publications: London).
Arbib, Michael A., and Ernest G. Manes. 1975. Arrows, Structures, and Functors: The Categorical Imperative (Academic Press: New York).
Aristotle. 1996. Physics (Oxford University Press: Oxford).
Baez, John C. 1997. “An Introduction to n-Categories.” In 7th Conference on Category Theory and Computer Science, edited by E. Moggi and G. Rosolini, 1-33. Springer, Berlin.
Barandiaran, Xabier, Ezequiel Di Paolo, and Marieke Rohde. 2009. ‘Defining Agency: individuality, normativity, asymmetry and spatio-temporality in action’, Journal of Adaptive Behavior (Rohde, M. & Ikegami, T, (Eds) Special Issue on Agency): 1-13.
Beer, Stafford. 1981. Brain of the Firm – 2nd Edition (John Wiley & Sons: Chichester, UK).
Boxer, Philip J. 2023. “In which socio-technical open systems reach a limit.” In Asymmetric Leadership. https://asymmetricleadership.com/2023/10/24/in-which-socio-technical-open-systems-reach-a-limit/.
Gilbert, Scott F. 2012. ‘A Symbiotic View of Life: We Have Never Been Individuals’, The Quarterly Review of Biology, 87: 325-41.
Hirschhorn, L. 1999. ‘The Primary Risk’, Human Relations, 52: 5-23.
Kineman, John J. 2008. “Fundamentals of Relational Complexity Theory.” In 52nd Annual Meeting of the ISSS Madison, Wisconsin.
———. 2009. “Relational Theory and Ecological Niche Modeling.” In 53rd Meeting of the ISSS. University of Queensland, Brisbane, Australia.
———. 2011. ‘Relational Science: A Synthesis’, Axiomathes, 21: 393-437.
———. 2018. ‘Four Kinds of Anticipatory (M-R) Life and a Definition of Sustainability.’ in R. Poli (ed.), Handbook of Anticipation (Springer Nature: Switzerland).
Kineman, John J., Béla A. Bánáthy, and Judith Rosen. 2007. “The Atomistic Structure of Relationship: Rosen’s Implicate Order.” In Proceedings of the 51st Annual Meeting of the ISSS. Tokyo, Japan.
Krupanidhi, Srirama, N. Madhan Sai, Homan Leung, and John J. Kineman. 2017. ‘The Leaf as a Sustainable and Renewable System’, Systems Research and Behavioural Science, 34: 564-76.
Luhmann, Niklas. 2013[2002]. Introduction to Systems Theory (Polity: Cambridge, UK).
Maturana, Humberto R., and Francisco J. Varela. 1980[1972]. Autopoiesis and Cognition: The Realization of the Living (D. Reidel Publishing Company: London).
Rosen, R. 1958. ‘A Relational Theory of Biological Systems’, Bulletin of Mathematical Biophysics, 20: 245-60.
———. 1974. “On Biological Systems as Paradigms for Adaptation.” In The Political, Social, Educational and Policy Implications of Structuralisms. Adaptive Economic Models.
———. 1985. Anticipatory Systems (Pergamon Press: New York).
———. 1991. Life Itself (Columbia University Press: New York).
———. 2000. Essays on Life Itself (Columbia University Press: New York).
Singh, Yadvir, Javed Ahmad, Javed Musarrat, Nasreen Z. Ehtesham, and Seyed E. Hasnain. 2013. ‘Emerging importance of holobionts in evolution and in probiotics’, Gut Pathogens, 22: 5-12.
Spencer-Brown, G. 1979[1969]. Laws of Form (E.P. Dutton: New York).
Ulanowicz, Robert E. 2000. ‘Ontic Closure and the Hierarchy of Scale.’ in J.L.R. Chandler and Gertrudis Van de Vijver (eds.), Closure: Emergent Organisations and Their Dynamics (Annals of the New York Academy of Sciences).
———. 2019. ‘The tripartite nature of causalities in ecosystem dynamics’, Current Opinion in Systems Biology, 13: 129-35.
Van de Vijver, Gertrudis. 1998. ‘Evolutionary Systems and the Four Causes: A Real Aristotelian Story?’ in Gertrudis Van de Vijver, Stanley N. Salthe and Manuela Delpos (eds.), Evolutionary Systems: Biological and Epistemological Perspectives on Selection and Self-Organization (Springer Science+Business Media: Dordrecht).